10456. Server
Amin and Murad decided to create a
Minecraft game server.
They invited k guests to the grand
opening of the server. The guests live in different cities, and when connecting
to the server, they will experience a certain latency (ping) depending on their
location. Realizing the potential issues, Amin and Murad decided to choose the
most optimal location for hosting the server.
There are n cities, numbered from 1
to n, and m bidirectional communication channels between them. A
connection to the server is only possible through these channels. Using them,
it is possible to establish a connection between any two cities. Each pair of
cities may have at most one direct communication channel, and no city is
connected to itself. Each channel has a transmission delay of wi.
The connection delay between a city and the
server is defined as the minimum possible sum of delays along the path from
that city to the server.
Amin and Murad want to choose a city to
host the server so that the total connection delay for all guests is minimized.
If the server is hosted in the same city where a guest lives, the delay for
that guest is considered to be zero.
If there are multiple cities with the same
minimum total delay, Amin and Murad will choose the city with the smallest
number.
Determine the city where the server will be
hosted and the total connection delay for all guests to the server.
Input.
The first line
contains three integers n (1 ≤ n ≤ 104), m
(1 ≤ m ≤ 4 * 104), and k (1 ≤ k ≤ 100) –
the number of cities, the number of communication channels, and the number of
guests, respectively. The second line contains k distinct integers ci (1 ≤ ci
≤ n) – the numbers of the
cities where the guests live.
Each of the following m lines
contains three integers ui, vi, and wi (1 ≤ ui, vi
≤ n)
– describing a bidirectional communication channel between cities ui
and vi with a delay of wi (1 ≤ wi ≤ 104).
Output. Print two integers – the number of the city where the
server will be hosted, and the total connection delay for all guests to this
server.
|
Sample
input |
Sample
output |
|
5 6 3 1 2 5 1 2 10 1 4 3 2 4 2 2 5 8 3 4 5 3 5 3 |
2 13 |
SOLUTION
graphs - Dijkstra
Algorithm analysis
Since n ≤ 104, we will represent the
graph using an adjacency list.
Run Dijkstra’s algorithm
from each city where a guest resides. For every vertex, compute the sum of
distances to all guest cities.
The vertex with the
smallest sum will be the optimal location for hosting the server. If there are
multiple such vertices, choose the one with the smallest number.
Note that the server does
not necessarily have to be placed in a city where one of the guests lives.
Example
The graph given
in the example is as follows:
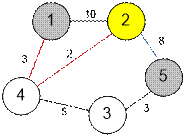
Run Dijkstra’s algorithm
from the vertices where the guests reside: 1, 2, and 5. For each of these
vertices, determine the shortest distances to all other cities.
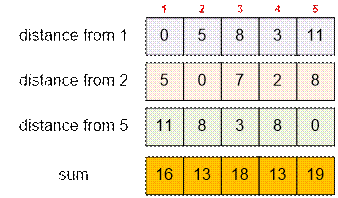
Next, for each vertex of
the graph, compute the sum of distances to all the cities with guests. The
minimum sum of distances is 13, and it is achieved at the vertex with the
smallest number 2.
Therefore, the server
should be placed in city 2. The total distance from it to the cities where the
guests reside is 5 + 0 + 8 = 13.
Algorithm implementation
Declare a constant for infinity.
#define INF 0x3F3F3F3F
The edge structure will store information about an edge: the
vertex node that the edge leads to, and the weight dist of the
edge.
struct edge
{
int node, dist;
edge(int node, int dist) : node(node), dist(dist) {}
};
Declare a comparator for sorting pairs (node, dist) in descending order of
the dist value.
bool operator< (edge a, edge b)
{
return a.dist > b.dist;
}
Declare an adjacency list to represent the graph.
vector<vector<edge> > g;
The Dijkstra function implements Dijkstra’s algorithm. It takes
the graph g and the starting vertex start as input. The return
value is an array d, where d[i] contains the shortest distance
from the vertex start to vertex i.
void Dijkstra(vector<vector<edge> >& g, vector<int>& d, int start)
{
priority_queue<edge> pq;
pq.push(edge(start, 0));
d = vector<int>(n + 1, INF);
d[start] = 0;
while (!pq.empty())
{
edge e = pq.top();
pq.pop();
int v = e.node;
if (e.dist > d[v]) continue;
for (auto e : g[v])
{
int to = e.node;
int cost = e.dist;
if (d[v] + cost < d[to])
{
d[to] = d[v] + cost;
pq.push(edge(to, d[to]));
}
}
}
}
The main part of the program. Read the input data.
scanf("%d %d %d", &n, &m,
&k);
c.resize(k);
for (i = 0; i < k; i++)
scanf("%d", &c[i]);
Read the input weighted graph.
g.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d %d %d", &a, &b, &w);
g[a].push_back(edge(b, w));
g[b].push_back(edge(a, w));
}
Run Dijkstra’s algorithm from the cities where the guests live.
dp.resize(n + 1);
for (i = 0; i < k; i++)
{
Dijkstra(g, dist, c[i]);
for (j = 1; j <= n;
j++)
dp[j] += dist[j];
}
Currently, dp[i] contains the sum of the shortest distances from
vertex i to all the cities where the guests are located. The next step
is to find the minimum value among the elements of the dp array and print
the corresponding result. The variable ptr stores the smallest vertex
number where the server should be placed.
res = INF;
for (i = 1; i <= n; i++)
{
if (dp[i] < res)
{
res = dp[i];
ptr = i;
}
}
Print the answer.
printf("%d %d\n", ptr, dp[ptr]);